Evaluation Home Page |
| Information on mass chains and nuclides |
|
 |
A = 17 Theoretical Discussion
Because much of the theoretical work reported in the literature for A = 17 is relevant to more than one of the A = 17 nuclides, the following general theoretical discussion for this mass system is provided here. Some of this work is also referenced in later sections of this compilation.
Ground state properties of 17O and 17F are calculated by (1989FU05) with the use of self-consistent relativistic mean field models of baryon-meson dynamics, including contributions from ρ, ω, and σ mesons. They calculate binding energies, rms radii, magnetic and quadrupole moments, and elastic magnetic scattering form factors and compare to experimental data. Work reported in (1990LO11) revisits previous calculations based on the density functional method. Binding energies of 17O and 17F as well as proton and neutron radii are calculated and compared to experimental data. Calculations of Coulomb excitation of the first excited state of 17O due to virtual E1 transitions through intermediate states are reported in (1989BA60). They use shell-model wavefunctions including single-particle harmonic oscillator and higher configurations. The work in (1986PO06, 1987RI03, 1989VOZM) deals with A = 17 nuclei as reaction products in heavy ion reactions. (1989WA06) reports shell model calculations which use a modification of the Millener-Kurath interaction (MK3), including energy spectra and wavefunctions of 17C and 17N. The half-life and decay modes of both the allowed and first-forbidden β-decays of 17C are predicted, as are the spectroscopic factors and electromagnetic transition rates of 17N. They find generally good agreement with experimental results.
Analog correspondences and structure of states in 17N and
17O are covered in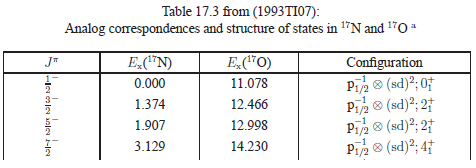 
17.3 (in PDF or PS). A relativistic Hartree
calculation was performed by (1991ZH06). The effect of tensor
coupling of the pion is found to be important in calculating the
magnetic moments. Results are presented for binding energies,
quadrupole moments, magnetic moments, and single particle energies.
(1988BR11) analyze ground state binding energies and
excited-state
energies using several two-body interactions. They develop a
semi-empirical "best fit" based on a 14-parameter
density-dependent two-body potential. (1988MI1J) discuss features of
an effective interaction used to calculate cross-shell matrix
elements. They apply shell-model transition densities to the
1ℏω excitation of non-normal-parity states in electron,
nucleon, and pion scattering. (1986YA1B) obtain an effective
shell-model interaction by starting with a bare Hamiltonian of
kinetic energy and the Reid soft-core pair potential, and folding
this with pair correlation operators not represented by
configuration mixing in a given shell model space. In (1987BR30),
calculations based on the full-basis sd-shell wave function are used
to analyze M1 transition data and magnetic moment data. The
parameters of an effective M1 operator are obtained. Differences in
effective operators are used to evaluate the importance of meson
exchange currents, Δ-isobar effects and other mesonic
exchange currents. The authors of (1986ED03) apply the particle-hole
model to the study of E1 states below the GDR using the WMBH
residual interaction and compare the results to experimental data.
The elastic magnetic form factor is calculated with the inclusion of
both the 2ℏω particle-hole excitations and the Zuker-type
multi-particle-multi-hole configuration mixing, the latter of which
helps explain the M3 suppression, but produces magnetic moments
which are too small (1992ZH07). The low-energy spectra were
investigated by (1990LI1Q), who included 2h-1p multiple scattering and
PH TDA self-screening in their Paris-potential-based Green's
function calculation. Two- and three-fragment clustering of
1p-shell nuclei is studied in the framework of the
intermediate-coupling shell model (1992KW01). (1991SK02) use matrix
inversion techniques to determine effective matrix elements for E2
and M1 transitions for A = 17 nuclei. A compilation of calculated
mass excesses and binding energies of members of T ≤ 6 isospin
multiplets for 9 ≤ A ≤ 60 is presented in (1986AN07). The
production of nuclei far from stability via multinucleon transfer
reactions is reviewed in (1989VOZM).