Evaluation Home Page |
| Information on mass chains and nuclides |
|
 |
16C (1993TI07)
(See Energy Level Diagrams for 16C)
GENERAL: See 
16.1 [General Table] (in PDF or PS) and 
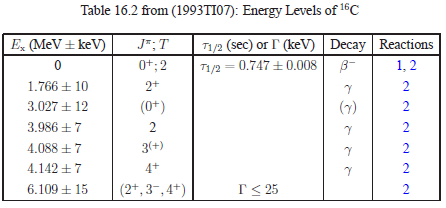16.2 [Table of Energy Levels] (in PDF or PS) here.
| 1. 16C(β-)16N | Qm = 8.012 |
The half life of 16C is 0.747 ± 0.008 sec. It decays to
16N*(0.12, 3.35, 4.32) [Jπ = 0-, 1+,
1+]: see 
16.3 (in PDF or PS) and (1993CH06). See also (1986AJ04) and see (1986KI05,
1988WA1E, 1992WA1L) for
theoretical discussions of extended shell-model calculations of
0+ → 0- transitions and determination of the
mesonic enhancements εmec of the
time-like component of the axial current. See also (1992TO04)
and see 16N, reaction 1.
| 2. 14C(t, p)16C | Qm = -3.013 |
States of 16C observed in this reaction are displayed in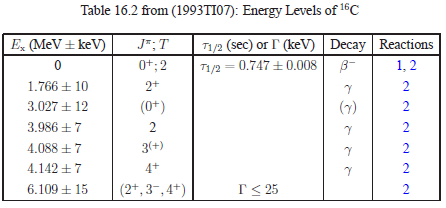
16.2 (in PDF or PS). See also 
16.3 (in
PDF or PS) of (1982AJ01).
| 3. 16O(K-, π+)Σ16C |
(1985BE31) used negative kaons of 450 MeV/c to produce Σ hypernuclear states, which they interpreted as Σ- particles in the p3/2 and p1/2 orbits of the Σ16C hypernucleus. Their energy splitting was used to constrain the Σ- spin-orbit coupling.
(1986HA26) performed a systematic shell-model analysis of Σ-hypernuclear states, in which they deduced a ΣN-spin-orbit interaction about twice as strong as the one for the nucleon. (1986MA1J) reached a similar conclusion after extracting the one-particle spin-orbit splitting εΣ = εΣp1/2 - εΣp3/2. (1987WU05) used the continuum shell-model to study competition between resonant and quasi-free Σ-hyeprnuclear production. The observed structures in the excitation spectra are essentially accounted for by the quasi-free mechanism alone. (1989DO1I) perform a series of shell model calculations of energy spectra of p-shell Σ hyeprnuclei, starting with several different parameterizations of the ΣN effective interaction. Production cross sections are estimated using DWBA. They suggest experiments to resolve open questions regarding the ΣN and Σ-nucleus interactions. (1989HA32) uses the recoil continuum shell model to calculate in-flight Σ hyernuclei production of this reaction (and others). The needed to modify the ΣN central interaction to fit data.
Coupled channels (CC) calculations for Σ-hypernuclear spectra give an energy integrated cross section which is about 1.7 times the experimental value (1987HA40). (1988HA44) report CC calculations emphasizing the proper treatment of the Σ continuum states. They find that a weak Σ central potential and a comparable ΣΛ conversion potential are required to describe experiment.